正文
1 | fun binarySearch(nums: IntArray, target: Int): Int { |

1 | fun binarySearch(nums: IntArray, target: Int): Int { |
1 | fun backtrack(...) { |
1 | fun dp(n: Int, memo: IntArray): Int { |
1 | class TrieNode { |
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
1 | 输入:nums = [2,7,11,15], target = 9 |
示例 2:
1 | 输入:nums = [3,2,4], target = 6 |
示例 3:
1 | 输入:nums = [3,3], target = 6 |
提示:
2 <= nums.length <= 10^4-109 <= nums[i] <= 10^9-109 <= target <= 10^9进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
1 | 这道题的关键在于对 hashmap 查找时间复杂度 O(1) 的应用 |
1 | class Solution { |
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
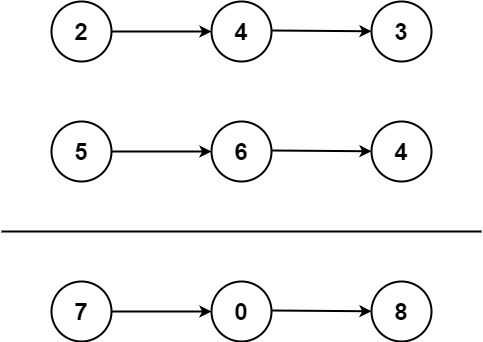
1 | 输入:l1 = [2,4,3], l2 = [5,6,4] |
示例 2:
1 | 输入:l1 = [0], l2 = [0] |
示例 3:
1 | 输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] |
提示:
[1, 100] 内0 <= Node.val <= 91 | 遍历两个链表,元素相加生成新列表。 |
1 | class Solution { |
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
1 | 输入: s = "abcabcbb" |
示例 2:
1 | 输入: s = "bbbbb" |
示例 3:
1 | 输入: s = "pwwkew" |
提示:
0 <= s.length <= 5 * 10^4s 由英文字母、数字、符号和空格组成1 | 巧妙的使用 HashMap<Char, Int> 记录每个字符的最新的位置 |
本题的巧妙在于使用 HashMap 和 遍历指针构建了一个滑动窗口
在寻找滑动窗口的时候,我们总是固定住一端位置去寻找另一端的位置,通常需要我们找到两个端点之间的关系
来分析滑动窗口的性质:左边届位置,右边界的位置,滑动窗口的长度
三者有以下这些关系:滑动窗口的长度 = 滑动窗口右边届 - 滑动窗口左边界
无论算法如何变化,我们知二求一
我们分析,遍历指针和左右边界的关系有三
情况一:遍历指针是滑动窗口的左边界
情况二:遍历指针是滑动窗口的右边界
情况三:遍历指针在滑动窗口的中间
结合滑动窗口的性质
情况一:知道窗口的长度,以遍历指针为左边界
情况二:窗口长度不固定,新增的元素决定窗口的长度,也就是左边界的位置
情况三:对于滑动窗口算法,通常情况下遍历指针要么位于窗口的左边界,要么位于右边界,用于控制窗口的扩展和收缩。在常规的滑动窗口算法中,遍历指针并不位于窗口的中间位置。
显然这种是情况二
当滑动窗口的位置和长度变化受制于新增的元素时,我们将遍历指针设置为
1 | class Solution { |
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
1 | 输入:nums1 = [1,3], nums2 = [2] |
示例 2:
1 | 输入:nums1 = [1,2], nums2 = [3,4] |
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-10^6 <= nums1[i], nums2[i] <= 10^61 | 讨论在两个有序数组中寻找中位数的问题 |
首先思考我们是否可以避免全排序找到中位数
我们有一种想法就是通过比较元素的大小找到需要舍弃的元素
我们观察一个有序数组,我们准备两个区间 RSmall, RBig 分别存放这个数组的偏小值与偏大值(相对中位数而言)
分别用 left,right 指针从两头操作偏小值与偏大值,将他们依次放入对应的数组
直到 「偶数时 RSmall.size = RBig.size 或者 奇数时 RSmall.size = RBig.size + 1」,中位数显然易得
好,现在我们来看两个有序数组的复杂情况
我们同样准备两个区间 RSmall, RBig,同样我们需要将数组偏小值放进 RSmall,偏大值放进 RBig
与一个有序数组不同的是,现在我们必须综合考虑两个有序数组的情况
所以 RSmall 区间里可能既包含 num1 数组的偏小元素也包含 num2 数组的偏小元素,对于RBig也是一样
这就让我们的思考变得复杂了,这使得 RSmall,RBig 变得无序
现在将这个 RSmall 再细分为 RSmallN1 区间,以及 RSmallN2 区间,同样有 RBigN1,RBigN2 区间
想要得到中位数,那么偶数时 RSmall.size = RBig.size 或者 奇数时 RSmall.size = RBig.size + 1
也就有
「 必要条件一: 偶数时 RSmallN1.size + RSmallN2.size = RBigN1.size + RBigN2.size 奇数时 RSmallN1.size + RSmallN2.size = RBigN1.size + RBigN2.size +1 」
同时 RSmall 区间内任何一个元素都必须小于 RBig 区间
自然有 Small 区间的子区间的任何一个元素都小于 Big 区间的子区间的任何一个元素
所以得到
「 必要条件二: RSmallN1 的最大值 < RBigN1 的最小值 ( 因为数组有序,这是不用判断的 ) RSmallN1 的最大值 < RBigN2 的最小值 RSmallN2 的最大值 < RBigN1 的最小值 RSmallN2 的最大值 < RBigN2 的最小值 ( 因为数组有序,这是不用判断的 )」
简化一下
「 必要条件二: maxOf( RSmallN1 ) < minOf ( RBigN2 ) maxOf( RSmallN2 ) < minOf ( RBigN1 ) 」
显然必要条件一加上必要条件二就是充分必要条件
现在我们要得到这四个区间,或者说要在两个有序数组分别划分出这四个区间
我们要在这两个数组中分别找到关键的那个分隔元素
因为必要条件一的原因,我们找到了 num1 数组的分割元素,我们也就找到了 num2 数组的分割元素
这非常好理解,因为 Small 区间和 Big 区间的数量是固定的,RSmallN1 多了一个元素,RSmallN2 就要对应减少一个元素
所以我们只要找到 num1 数组的分隔元素即可
至此,问题成功转化成了
在 num1 数组中查找出一个关键元素位置,这个关键元素满足上述两条必要条件
这是一个典型的有判断条件的查找问题,我们就可以使用二分查找,测试每个元素是否符合上述两个条件
关于二分查找这里不再赘述。
以下是基于二分查找的 Kotlin 代码实现,用于找出两个有序数组的中位数:
1 | // 该函数用于在两个已排序整数数组中找到它们的中位数,返回类型为 Double。 |
1 | fun findMedianSortedArrays(nums1: IntArray, nums2: IntArray): Double { |
留给大家一个问题,问 N 个有序数组的中位数怎么求?
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
1 | 输入:s = "babad" |
示例 2:
1 | 输入:s = "cbbd" |
提示:
1 <= s.length <= 1000s 仅由数字和英文字母组成1 | 介绍 Manacher 算法 |
数据预处理: 首先回文子串有两种形式 奇数 与 偶数 也就有两种对应的指针操作方式
假定有字符数组 ababaabc 改成 # a # b # a # b # a # a # b # c # 将偶数数组变成奇数统一处理 索性改成 ^ # a # b # a # b # a # a # b # c # $,头尾清晰
这样就可以通过把每个字符作为回文子串的中心向两边扩展,找出最长回文子串 时间复杂度是 O(n^2)
现在需要我们观察回文子串的规律,简化计算
1 | 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 |
情况一:
1 | 10 --^-- P[10] = 1 |
第 10 行,第 12 行 都是 第 11 行 的子串,完全包含在 第 11 行 之中,由于回文串的对称性 此时直接有 P[10] = P[12]
情况二:
1 | 4 ------^------ P[4] = 3 |
第 4 行,第 8 行 都是 第 6 行 的子串,分别位于字符串的两端,当我们知道 第 4 行 的信息之后,我们知道 第 8 行 至少有 第 4 行 那么长,至于会不会更长,继续试着向两边扩展即可 此时需要干两件事 1. 将 P[8] = P[4]; 2. 继续向外扩展
情况三: 8 ——^—— P[8] = 3 11 ——–^——– P[11] = 2 14 –^– P[14] = 1 第 8 行 部分与 第 11 行 重叠,第 14 行 是 第 11 行 的子串,非常简单,舍弃超出部分 8 –^– P[8] = 3 11 ——–^——– P[11] = 2 14 –^– P[14] = 1 当成这样处理即可 定义遍历指针 i ,指向回文的中心的指针 center 和 指向回文串右边界的指针 r 此时需要干两件事 1. 将 P[8] = r - i ; 2. 继续向外扩展
好,我们现在已经理解了 Manacher 算法的精髓了 我们思考一下算法该怎么写
P[i] 计算过程
1 | 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 |
我列出了每次计算面对的情况,计算的次数以及是否需要 r 我希望大家思考 当新计算出的 r 与旧的 r 相等时,是否应该更新 center ? 当然不应该,我们肯定更倾向于选择更长的回文串
是这样吗? 我们思考一种情况
1 | 2 --^-- p[2] = 1 |
第 6 行 较长有什么用呢,有用的只是 i 到 r 这一小截而已,不更新是因为都一样,没必要更新,所以只有当我们发现了更右边的 r 更新即可
1 | class Solution { |
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
1 | P A H N |
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
1 | string convert(string s, int numRows); |
示例 1:
1 | 输入:s = "PAYPALISHIRING", numRows = 3 |
示例 2:
1 | 输入:s = "PAYPALISHIRING", numRows = 4 |
示例 3:
1 | 输入:s = "A", numRows = 1 |
提示:
1 <= s.length <= 1000s 由英文字母(小写和大写)、',' 和 '.' 组成1 <= numRows <= 10001 | 重点不在字形,重点在变换是什么变换 |
我们思考,为什么这个算法难写
分析 N字形 的离散函数,我们面临着一个唯一的 x 对应着 1- N 个 y
在 x 变化的时候,我们首先要算该 x 对应了几个 y
这根本不符合函数的定义函数是指一个集合中的每个元素都有且仅有一个映射到另一个集合中的元素,这种关系被称为函数映射
推出我们需要把一个一维度线性离线函数 s = f(n) 变成二维离散函数 s = g(x, y)
注意,这里好玩的是 y 和 x 其实是数列
即 s = g(x(n), y(n))
我们开始推导
1 | x(n) = x(n-1) + 1 |
1 | class Solution { |